1. Matlab 맛보기 ¶
% 마방진
>> A = magic(3)
A =
8 1 6
3 5 7
4 9 2
% 역행렬
>> B = inv(A)
B =
0.1472 -0.1444 0.0639
-0.0611 0.0222 0.1056
-0.0194 0.1889 -0.1028
>> A*B
ans =
1.0000 0 -0.0000
-0.0000 1.0000 0
0.0000 0 1.0000
%Deteminent(?)
>> det(A)
ans =
-360
% Eigen Value
>> [V, D] = eig(A)
V =
-0.5774 -0.8131 -0.3416
-0.5774 0.4714 -0.4714
-0.5774 0.3416 0.8131
D =
15.0000 0 0
0 4.8990 0
0 0 -4.8990
%help comet을 치면 나오는 예제. 애니메이션 그래프가 출력된다.
>> t = -pi:pi/200:pi;
>> comet(t,tan(sin(t))-sin(tan(t)))
>> peaks
>> vibes
3. MS word와의 연동 ¶
- >> notebook : MS word 실행
- Matlab 함수 타이핑 → 마우스로 긁어서 블럭지정 → 우클릭 메뉴 불러오기 → Evaluate Cells → 해당 함수가 수행되며, 결과가 자동으로 MSword에 삽입된다.
- plot을 수행할 경우 그래프도 자동으로 포함된다.
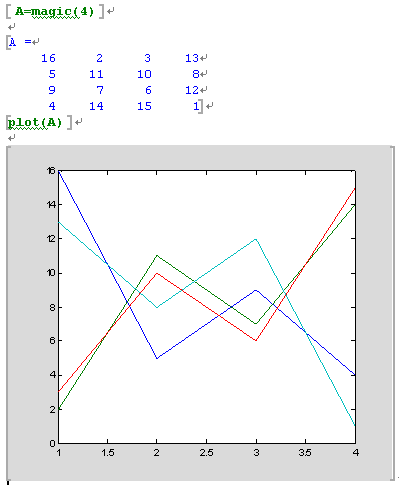
[PNG image (7.31 KB)]
4. Shortcut Toolbar ¶
자주 사용하는 Shortcut을 등록해서 사용할 수 있다.
Shortcut Toolbar위에서 우클릭 메뉴를 불러온 뒤, New Shortcut을 클릭하면 새로운 Shortcut을 생성할 수 있다.
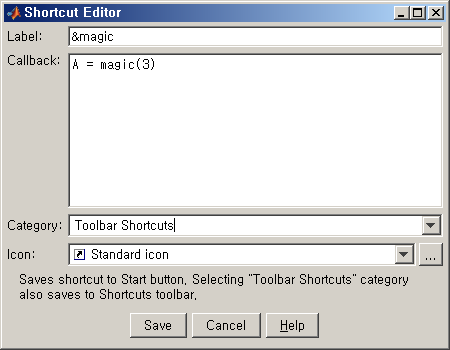

[PNG image (5.7 KB)]
5. Cell Toolbar ¶
Matlab Editor에서 주석문자인 %%을 사용해서 Cell을 구분할 수 있다. 한 Editor안에서 구분된 Cell은 따로 실행할 수 있다.

%를 하나만 사용할 경우에는 주석으로만 사용된다.

[PNG image (1.31 KB)]
6.1.1. lookfor ¶
함수명은 모르지만, 핵심 키워드는 알고 있을 경우 사용하는 함수명 검색 명령
lookfor fourier -all 을 사용하면 관련된 모든 함수가 출력된다.
>> lookfor fourier FFT Discrete Fourier transform. FFT2 Two-dimensional discrete Fourier Transform. FFTN N-dimensional discrete Fourier Transform. IFFT Inverse discrete Fourier transform. IFFT2 Two-dimensional inverse discrete Fourier transform. IFFTN N-dimensional inverse discrete Fourier transform. fi_radix2fft_demo.m: %% Fixed-Point Fast Fourier Transform (FFT) DFTMTX Discrete Fourier transform matrix. SPECGRAM Spectrogram using a Short-Time Fourier Transform (STFT). SPECTROGRAM Spectrogram using a Short-Time Fourier Transform (STFT). FFT Quantized Fast Fourier Transform. FOURIER Fourier integral transform. IFOURIER Inverse Fourier integral transform.
6.1.2. help ¶
함수명을 알고 있으며, command window에서 간단한 설명을 보고 싶을 때 사용
>> help fft
FFT Discrete Fourier transform.
FFT(X) is the discrete Fourier transform (DFT) of vector X. For
matrices, the FFT operation is applied to each column. For N-D
arrays, the FFT operation operates on the first non-singleton
dimension.
FFT(X,N) is the N-point FFT, padded with zeros if X has less
than N points and truncated if it has more.
FFT(X,[],DIM) or FFT(X,N,DIM) applies the FFT operation across the
dimension DIM.
For length N input vector x, the DFT is a length N vector X,
with elements
N
X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N.
n=1
The inverse DFT (computed by IFFT) is given by
N
x(n) = (1/N) sum X(k)*exp( j*2*pi*(k-1)*(n-1)/N), 1 <= n <= N.
k=1
See also fft2, fftn, fftshift, fftw, ifft, ifft2, ifftn.
Overloaded functions or methods (ones with the same name in other directories)
help uint8/fft.m
help uint16/fft.m
help qfft/fft.m
help iddata/fft.m
Reference page in Help browser
doc fft
6.2. Tab ¶
Command Window, Editor에서 명령어 일부를 타이핑하고 Tab을 누르면 관련 명령 목록이 주르륵 나타난다. 명령어 안의 변수들도 Tab을 사용할 수 있다.
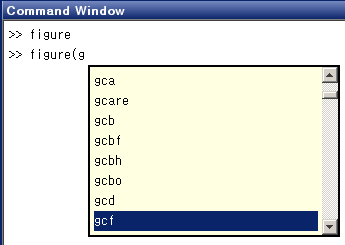

[PNG image (3.91 KB)]